Basic Algorithms in JavaScript (part 1)
Basic Algorithms in JavaScript (part 1)
Hi guys, long time no see!
Recently, I decided to go back to learn about basic stuff in Computer Science such as Data Structures and Algorithms, Algebra, Statistics, etc. in order to process to Advanced Machine Learning and Deep Learning. I took a course on Udacity named “Data Structures and Algorithms” and decided to write weekly blogs from what I have learned about Algorithms (as well as Machine Learning) for you guys to better understanding the Computer Science and possibly prepare for the Coding Interview. Hope this helps!
P/S: I tried my best to make this blog post as much comprehensive as possible. However, if you are in CS major and want to explore deeper in Algorithms, please do not hesitate to search for more resources. (Also, feel free to contact me if you have any questions/ideas, I am always eager to connect and discuss with you)
-Christopher Le-
I. Steps needed to remember while solving algorithm problems:
1. Clarify the question
2. Generate inputs and outputs
3. Generate test cases
4. Brainstorming
5. Run time analysis
6. Coding
7. Debugging
Remember to do all of them on whiteboard/paper or on computer but do not run the code
II. Quick review on some Data Structures’s concepts:
1.Lists:
Short description:
“Lists” are one type of data structure, and can store multiple values. They are unique in how they pair data with “pointers”, the pointers indicating the next piece of data’s memory location. In lists, data is stored in various disjointed locations memory. Because data is stored in different locations, each piece of data can only be accessed through the pointer that precedes it.
2. Arrays:
Short description:
“Arrays” are one type of data structure, and can store multiple values. Each element can be accessed through its index (a number that denotes its order within the data). Data is stored sequentially in memory in consecutive locations. Because they are stored in consecutive locations, memory addresses can be calculated using their indices, allowing for random access of data. Another feature of arrays is that adding or deleting data in a specific location carries a high cost compared to lists.
3. Stacks:
Short description:
The structure of a stack can be easily imagined as a pile of objects stacked vertically. When extracting these objects, they are extracted from the top down as the rule “LIFO” (“Last In First Out”). We use the term “Push” to refer to the act of adding data to stack, and the term “Pop”, in opposite, to refer to the act of extracting data from the stack.
4. Queues:
Short description:
“Queues” are also known as “waiting lines” like a group of people waiting in line. The sooner a person lines up, the higher their priority. This is called “First In First Out” (FIFO). We use the term “enqueue” to refer to the act of adding data to a queue, and “dequeue” for the act of extracting data from a queue
5. Hash Tables:
Short description:
“Hash Tables” are good at storing data in sets made of “keys” and “values”. By searching and extracting a key, we can learn its corresponding value. Hash Tables solve the problem when it takes time to search through data stored in an array, which is inefficient.
6. Heaps:
Short description:
“Heaps” are used when implementing a “priority queue”. In a priority queue, data can be added in any order. Conversely, when extracting data, the smallest values are chosen first. As for the rule of heaps, a child number is always greater than its parent number. If the parent number happens to be greater, the child and the parent swap. When extracting a number from a heap, the number on the top is removed (which is also the smallest).
7. Binary Search Trees (BST):
Short description:
The numbered points are called “nodes”. Binary search trees have 2 properties: 1. All nodes are greater than the nodes in their left subtree; 2. All nodes are smaller than the nodes in their right subtree.
Bonus: Binary search tree (BST)’s implementation:
**class** Node {
constructor(data) {
**this**.right = **null**;
**this**.left = **null**;
**this**.data = data; }
}
III. Basic Algorithms:
A. Sort:
Problem: sort an array of unordered numbers
1.Bubble sort:
Short description: As the scale moves from right to left, it will compare 2 numbers. If left number is greater than right number, the position of them are swapped. If not, the scale keep moving left without swapping anything. The swapping continues until all numbers have been sorted
Implementation in Javascript:
**function** BubbbleSort(array) {
**var** newArray = [];
**let** n = array.length;
**for** (**var** i = 0; i < n - 1; i++) {
** for** (**var** j = 0; j < n - i - 1; j++) {
** if** (array[j] > array[j + 1]) {
** var** temp = array[j];
array[j] = array[j + 1];
array[j + 1]= temp;
}
}
}
**return** newArray.concat(array)
}
Run-time analysis: O(n²)
2. Selection sort:
Short description: The minimum of the array will be moved to the left. After each number is sorted, the algorithm calculates the next minimum value of the left-over array and move it to the left. The process continues until all values have been sorted.
Implementation in Javascript:
**function** SelectionSort(array) {
** for** (**var** i = 0; i < array.length; i++) {
** let** min = i;
** for** (**var** j = i + 1; j < array.length; j++) {
** if** (array[min] > array[j]) {
min = j
}
}
** if** (i !== min) {
[array[ i ],array[min]]= [array[min],array[ i ]];
}
}
** return** array;
}
Run-time analysis: O(n²)
3. Merge sort:
Short description: The array is divided in groups of 2 until each values is separated individually. From each sub-box, the smallest value is compared with values from the next sub-box in order from left to right. After each sub-box is sorted, the process continues until it returns into a sorted array.
Implementation in Javascript:
function MergeSort(array) {
if (array.length < 2) {
return array;
}
var middle = Math.floor(array.length / 2);
var left = array.slice(0, middle);
var right = array.slice(middle);
function merge(left, right) {
let newArray = [];
while (left.length && right.length) {
if (left[0] < right[0])
{
newArray.push(left.shift());
} else {
newArray.push(right.shift());
}
}
return newArray.concat(left, right);
}
return merge(MergeSort(left), MergeSort(right));
}
Run-time analysis: O(nlog(n))
4. Quick sort:
In this case, last element is picked as pivot
Short description:
Implementation in Javascript:
function QuickSort(array) {
if (array.length <= 1) {
return array;
} else {
var left = [];
var right = [];
var newArray = [];
var pivot = array.pop();
var length = array.length;
for (var i = 0; i < length; i++) {
if (array[i] <= pivot) {
left.push(array[i]);
} else {
right.push(array[i]);
}
}
return newArray.concat(QuickSort(left), pivot, QuickSort(right));
}
}
Run-time analysis: O(nlog(n))
B. Search:
Problem: find a specific number in an array. If number is not found, return -1.
1.Linear search:
Short description: compare the number with each value in the array from lowest to highest index. The searching process stops when the number is found. If all values are gone through without locating the number, the algorithm return -1
Implementation in Javascript:
function LinearSearch(array, length, number)
{
for (var i = 0; i < n; i++)
{
if (array[i] == x)
{
return i;
}
}
return -1;
}
Run-time analysis: O(n)
2. Binary search:
Short description: The algorithm sorts the array then defines the range that the number maybe located in. This is more efficient as we don’t have to run through all values to search for the number.
Implementation in Javascript:
function BinarySearch(array, l, r, x)
{
if (r >= 1)
{
var mid = 1 + (r -1 )/2;
if (array[mid] == x)
{
return mid;
}
else if (array[mid] > x)
{
return BinarySearch(array, 1, (mid -1 ), x);
}
else
{
return -1;
}
}
}
Run-time analysis: O(log(n))
C. Graph:
Problem: find a path from A to G
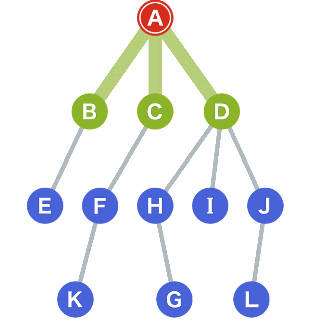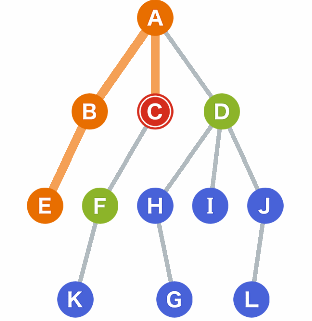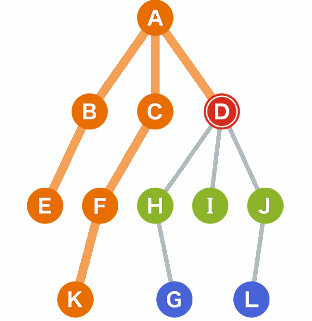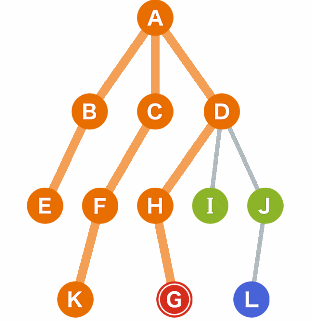
1. Breadth — First Search (BFS) //Graph Search:
Short description: A -> B -> C -> D -> E -> F -> H -> I -> J -> K -> G
From the parent, the process finishes searching in all nodes in a sub-parent before moving to next ones from left to right. The process continues until the destination is found.
Implementation in Javascript (@chrisco’s approach):
function bfs(value, tree) {
queue = [];
queue.unshift(tree);
while (queue.length > 0) {
curNode = queue.pop();
if (curNode.value === value) {
return curNode;
}
var len = curNode.children.length;
for (var i = 0; i < len; i++) {
queue.unshift(curNode.children[i]);
}
}
return null;
}
Run-time analysis: O(n²)
| Other approach’s run-time analysis: O( | V | ) |
2. Depth — First Search (DFS) //Graph Search:
Short description: A -> B -> E -> C -> F -> K -> D -> H -G
Like the name of the algorithm, DFS will search all nodes in terms of its depth of a parents from left to right. The process continues until the destination is found.
Implementation in Javascript (@chrisco’s approach):
function dfs(value, node) {
stack = [];
stack.push(node);
while (stack.length != 0) {
var curNode = stack.peek()
if (curNode.value == value) {
return curNode;
}
curNode.visited = true
stack.push(getFirstUnvistedNode(curNode));
}
}
Run-time analysis: O(n²)
| Other approach’s run-time analysis: O( | V | + | E | ) |
D. Other basic algorithm:
1.Recursion — Example with Fibonacci problem:
Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … (each number is the sum of the two preceding ones, starting from 0 and 1)
Problem: find Fibonacci value of nth element
function Fib(n)
{
| if (n == 0 | n == 1) { return 1;} |
return Fib(n - 1) + Fib (n - 2)
}
Run-time analysis: O(1.618^(n+1))
2. Euclidian Algorithm — Example with Finding GCD Problem:
GCD: greatest common divisor
Problem: find GCD of 2 numbers
function GCD(a, b) {
if(a === 0) { return b;}
if(b === 0) { return a;}
return GCD(b, a % b);
}
Run-time analysis: O(log(n)²)
**Github: **https://github.com/locvicvn/Algorithm
What to expect in Basic Algorithms in Javascript (part 2):
-
Dynamic Programming
-
Shortest Path Problem
-
Knapsack Problem
-
Divide and Conquer
-
Strings Keys
-
Traveling Salesman Problem
References:
-
“Data Structure and Algorithms” course on Udacity — Course’s link: https://classroom.udacity.com/courses/ud513
-
HackerRank Coding Interview on Youtube — Playlist’s link: https://www.youtube.com/playlist?list=PLOuZYwbmgZWXvkghUyMLdI90IwxbNCiWK
-
Big-O Notation Cheatsheet: https://www.hackerearth.com/practice/notes/big-o-cheatsheet-series-data-structures-and-algorithms-with-thier-complexities-1/
-
Short descriptions’ credits: http://www.algorithm.wiki
-
Credit for images: http://www.algorithm.wiki
-Christopher Le-