Almost all about that graph (part 1)
[Algorithm] Almost all about that graph (part 1)
Table of content:
I. Why graph II. What is graph III. Types of graph algorithms:
Part 1:
1. Graph traversal (BFS, DFS) 2. Finding the path with the lowest cost or shortest path (besides BFS) (Bellman-Ford, Dijkstra, Floyd-Warshall)
Part 2:
3. Minimum spanning tree (Prim, Union-Find) 4. Sorting (Topological sort) III. Example with a Leetcode problem
Part 3:
IV. Application in neural network — CNN (Building an image classification — Bonus topic) V. Conclusion
I. Why graph?
If you look closely at your smart phone’s applications or many other technical applications, the graph actually appears in every corner of our lives. From finding the shortest path from a location to another on Google Maps to graphing your connections on social media.

Finding an optimal graph algorithm will reduce a great amount of cost or compute resources when applying graph with real life’s great amount of data like millions of real world’s streets (example of finding the shortest path on Google Map). (Well, unless you are trying to calculate the shortest distance between you and your crush’s heart, can’t help you with that 😅)
II. What is a graph (in data structure and algorithm)?

-
A graph is a set of vertices and a collection of edges that each connect a pair of vertices. (Sedgewick, Algorithms 518)
-
There are two types of graph

- Loop and Multiple edges

A loop is an edge that connects a vertex to itself. If a graph has more than one edge joining some pair of vertices then these edges are called multiple edges.
- Simple Graph

A simple graph is a graph that does not have more than one edge between any two vertices and no edge starts and ends at the same vertex. In other words a simple graph is a graph without loops and multiple edges.
- Degree of a Vertex

6.Path
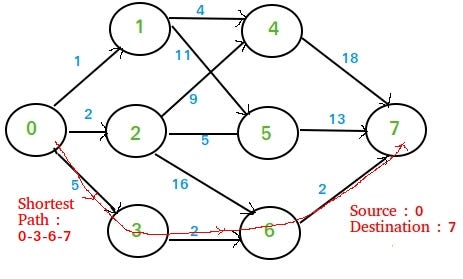
A path is a sequence of vertices with the property that each vertex in the sequence is adjacent to the vertex next to it. A path that does not repeat vertices is called a simple path.
- A Connected Graph

A graph is said to be connected if any two of its vertices are joined by a path. A graph that is not connected is a disconnected graph. A disconnected graph is made up of connected subgraphs that are called components
- Weight:

In a weighted graph, each vertex is assigned with a numerical value
- Adjacent matrix and Edge list representation:
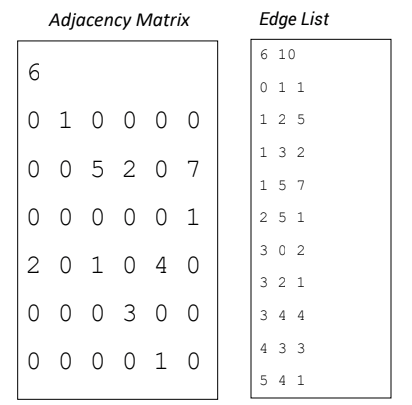
III. Types of graph algorithm:
1. Graph traversal:
Essential — BFS (breadth-first search) and DFS (depth-first-search)

DFS: begin from starting vertex to ending vertex, and repeat until all vertexes are covered.
BFS: begin from starting vertex to all vertexes but level by level.
a. Breadth-first search:

Description: BFS is used to find the shortest path from a vertex to another (these vertexes should be connected) or path from 1 vertex to other vertexes in a graph.
A great BFS demo by Sadanand Pai: https://sadanandpai.github.io/shortestpathfinder/
Detailed explanation: https://www.educative.io/edpresso/how-to-implement-a-breadth-first-search-in-python
Type of graph: undirected, directed, do not have weights (if not, weights are equal)
Algorithmic use cases: finding the shortest path between two nodes, testing if a graph is bipartite, finding all connected components in a graph, etc.
Complexity: O(V+E) — where V is the number of vertexes and E is the number of edges.
Code:
i. Implementing BFS:
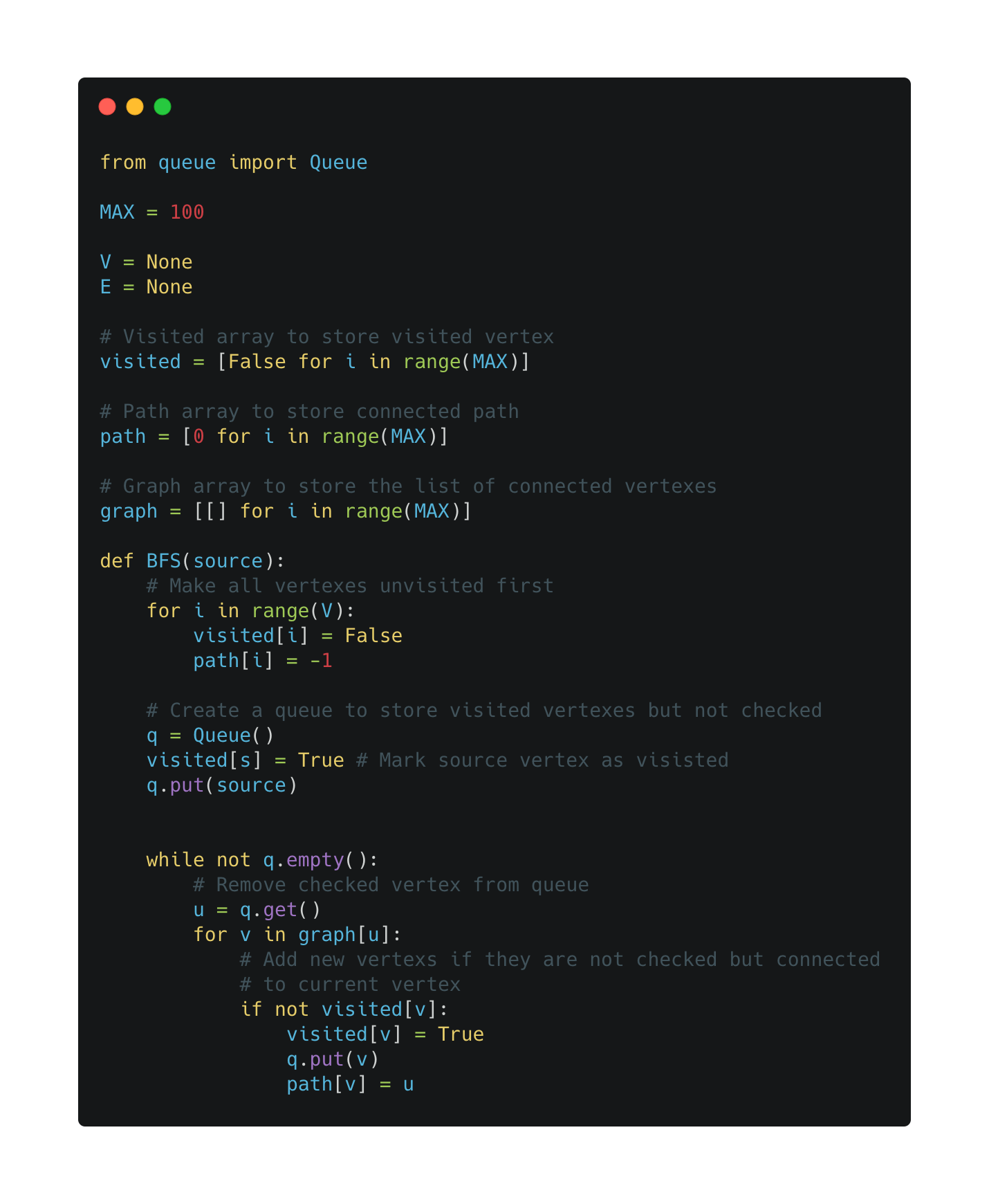
ii. Print path (2 methods):

iii. Example usage:

b. Depth-first search:

Description: DFS is used to find a path from a vertex to another (these vertexes should be connected). DFS solution is not necessarily the shortest path.
Detailed explanation: https://www.educative.io/edpresso/how-to-implement-depth-first-search-in-python
Type of graph: undirected, directed
Algorithmic use cases: topological sorting, solving problems that require graph backtracking, detecting cycles in a graph, finding paths between two nodes, finding an exit of a maze, etc.
Complexity: O(V+E)
Code:
i. Implementation:

ii. Example usage:

2. Finding the path with the lowest cost or shortest path (besides BFS):
In this chapter, for each edge, there will be a weight (cost) between two vertexes.
a. Bellman-Ford

Description: [Single-source] To find the path with the lowest cost from one vertex to every other vertex. Can be used to detect negative-weight cycle
Detailed explanation: https://www.geeksforgeeks.org/bellman-ford-algorithm-simple-implementation/
Type of graph: undirected, directed, have weights, weights can be positive or negative
Complexity in this implementation: O(V.E)
Code:
i. Implementation:

ii. Example usage:

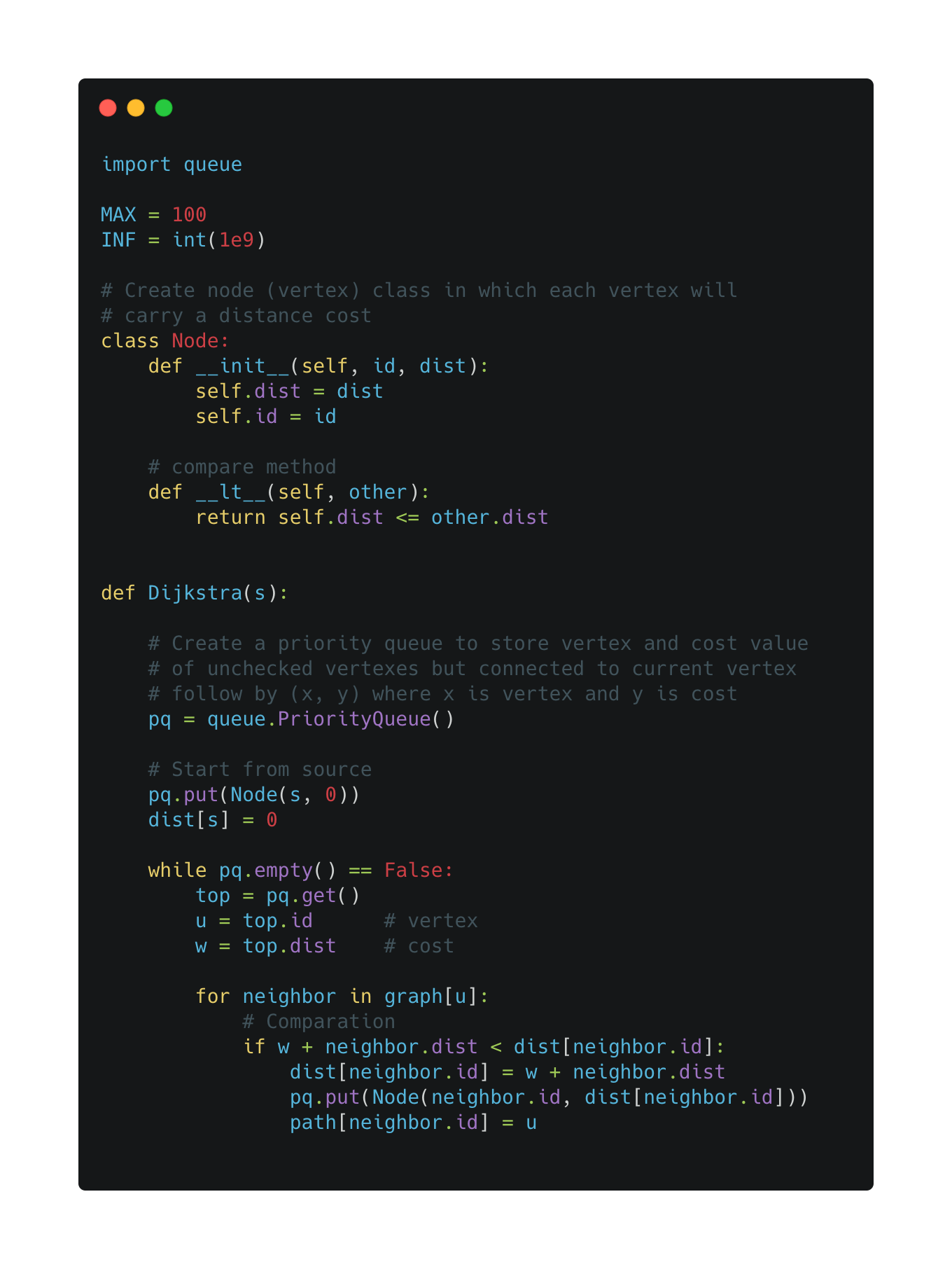
b. Dijkstra

Description: [Single-source] Dijkstra is used to finding a path with the lowest cost from one vertex to every other vertex.
Detailed explanation: https://www.bogotobogo.com/python/python_Dijkstras_Shortest_Path_Algorithm.php
Type of graph: undirected, directed, have positive weights
Complexity: O(V²) — optimal: O(ElogV) with a heap (priority queue)
Code:
c. Floyd-Warshall

Description: [All-pairs] Floyd-Warshall is used to finding the shortest path for all pairs of vertexes.
Detailed explanation: https://www.programiz.com/dsa/floyd-warshall-algorithm
Brief explanation:
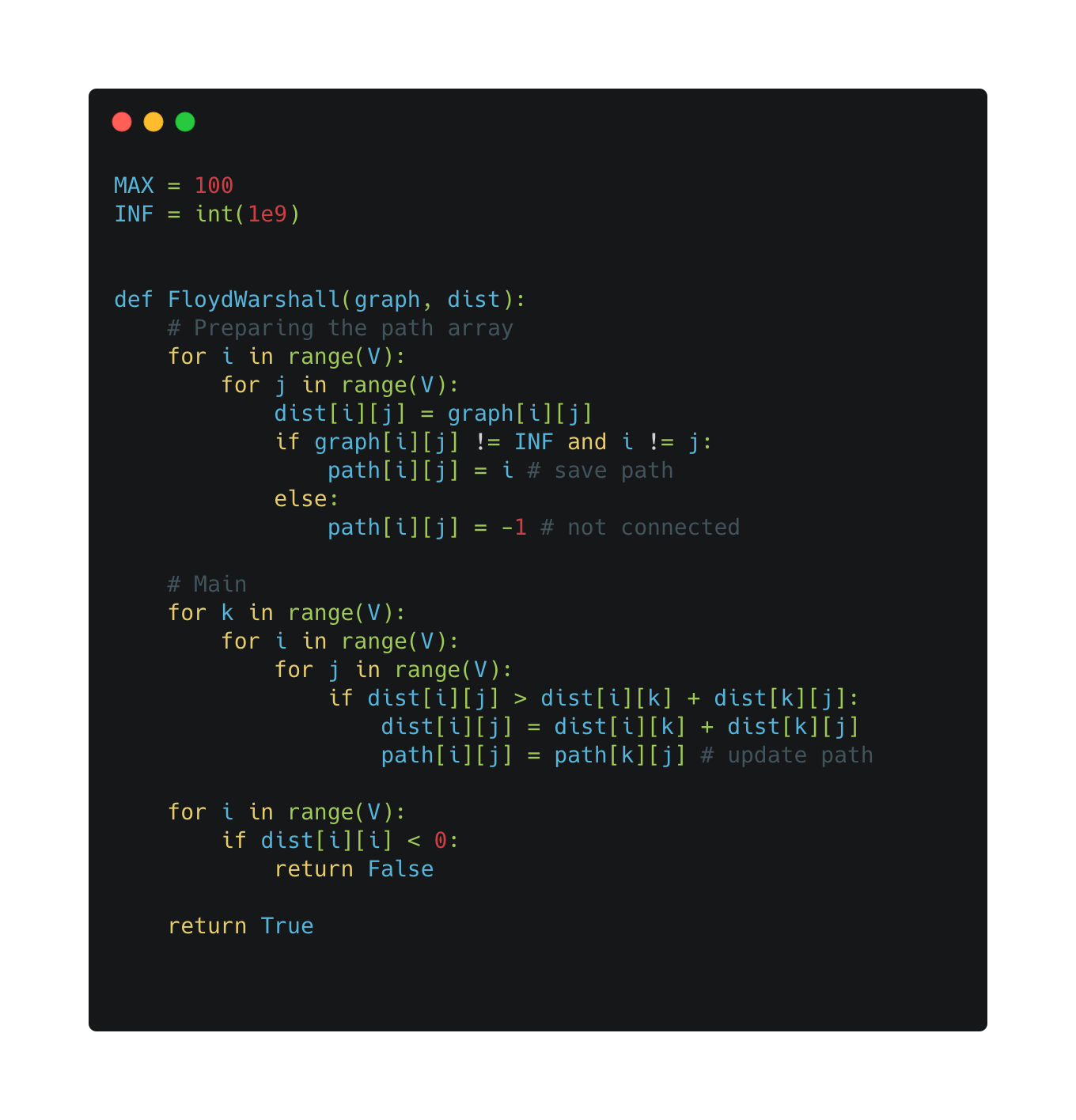
Floyd-Warshall uses Dynamic Programming method to save initial results into an array. Then it will run a loop again to check middle vertexes and their cost between themselves and starting and ending vertex. If current cost > (new cost 1 (start tonew vertex) + new cost 2 (new vertex to end)) then the current cost will update itself with (new cost 1 + new cost 2)
Type of graph: directed only, weights can be negative or positive, cannot be used in the negative cycle
Complexity: O(V³)
Code:
i. Implementation
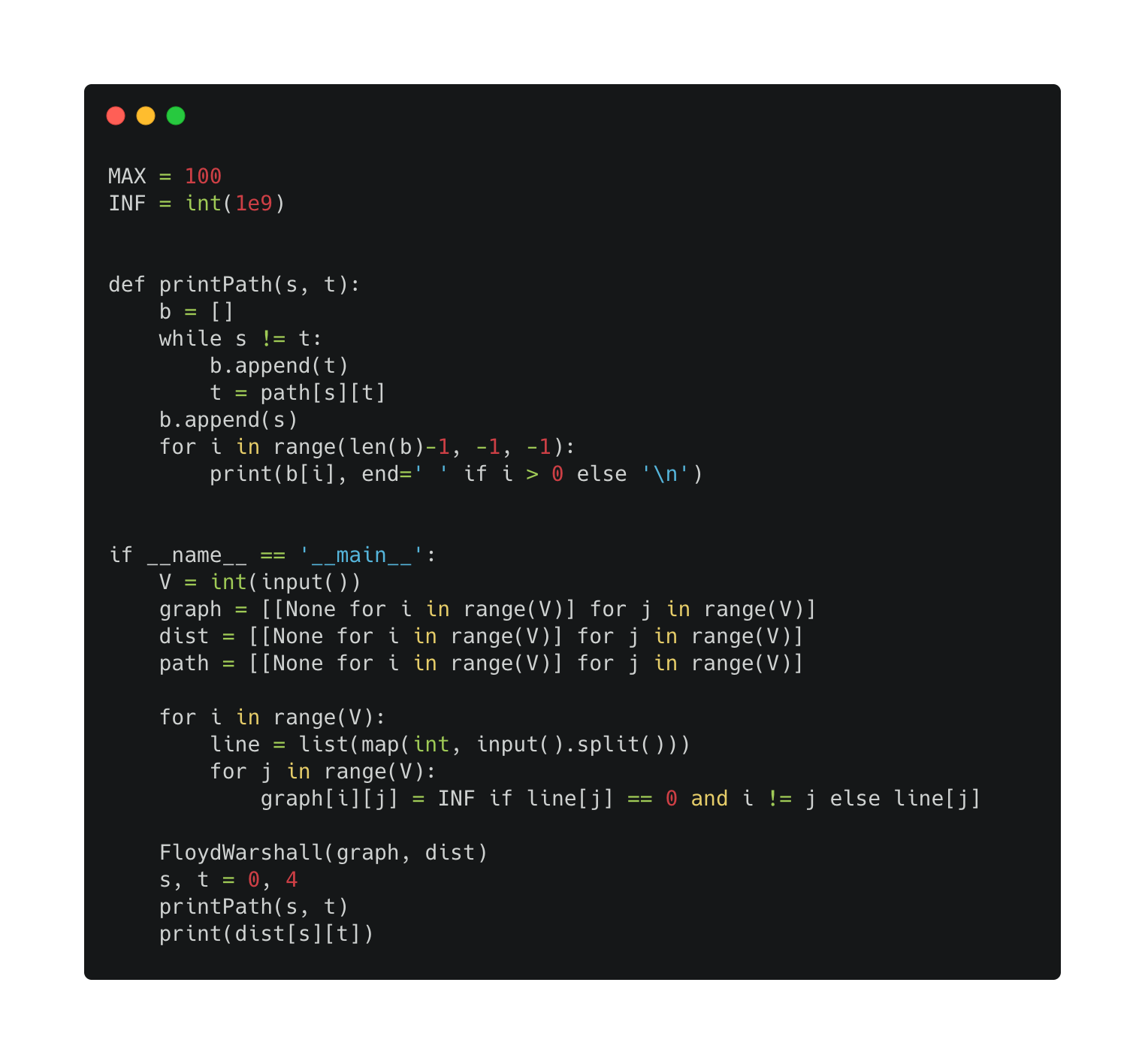
ii. Sample usage:
Summary:
Hope that this blog can help you understand more about graph algorithms and when to use them specifically.
Here is the overview. Stay tuned for part 2.
For better visualization, I strongly recommend this site: https://visualgo.net/en

Reference:
-
Sedgewick, R., Wayne, K. (2011). Algorithms, 4th Edition. Addison-Wesley. ISBN: 978–0–321–57351–3
-
CS 97SI: Introduction to Programming Contests from Stanford University
-
Big-O Coding Algorithm Class
For any questions or concerns, please contact me at locvicvn1234@gmail.com
My LinkedIn: https://www.linkedin.com/in/chrislevn/
My Coding Challenges: https://github.com/chrislevn/Coding-Challenges